Looking Good on Course Evaluations

• Columns,Taking a Chance in the Classroom

Mine Çetinkaya-Rundel, Kari Lock Morgan, and Dalene Stangl

At the end of each semester, students provide feedback on their courses via anonymous course evaluations. However, use of student evaluations as indicators of quality of the course and teaching effectiveness is often criticized since these measures may be reflecting biases in favor of nonteaching-related characteristics, such as the physical appearance of the instructor.

The 2005 Economics of Education Review article titled “Beauty in the Classroom: Instructors’ Pulchritude and Putative Pedagogical Productivity” finds that instructors who are viewed to be better looking receive higher instructional ratings. This article and the accompanying data set are relatable to students since they have first-hand experience evaluating courses and professors. They also have pre-existing notions about how some of the variables in the data set (e.g., class size, whether the professor is a native speaker, etc.) might affect their learning. Last, almost all students are familiar with RateMyProfessors.com, an online destination for professor ratings, where students rate their professors on, among other factors, hotness.

The Data

The study uses data from end of semester student evaluations for a large sample of professors from The University of Texas at Austin. These data are merged with descriptors of the professors and the classes. In addition, six students rate the professors’ physical appearance.

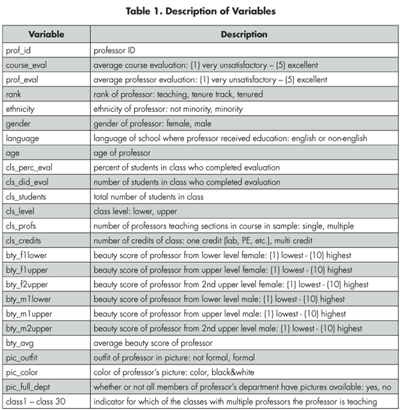
A list of the variables in the data set and their descriptions are provided in Table 1, and the complete data set can be found in the supplemental material. This is a slightly modified version of the original data set that was released as part of the replication data for Data Analysis Using Regression and Multilevel/Hierarchical Models.

Ideas for Using the Data in the Classroom

This data set/paper combination is approachable enough to be used in an introductory statistics course and complex enough to be used in an advanced undergraduate or graduate course on multilevel/hierarchical modeling.

The complexity of the data comes from the study design. The researchers first sampled 94 professors, and then collected data on courses they taught over a two-year period between 2000 and 2002. This sampling scheme resulted in 463 classes, with the number of classes taught by a unique professor in the sample ranging from 1–13. Therefore, the observations in this data set (classes) are not truly independent. While this is an interesting problem to tackle in an advanced course, we suggest treating the cases as independent observations when using this data set in more elementary courses. However, while students in these lower-level courses may not have the tools to correctly handle the hierarchical structure of the data, it is important for them to read the original paper to evaluate whether this simplifying assumption is actually reasonable and gain important insights into the data.

We have used this data set as part of a final project in an introductory statistics course (that covers multiple regression). Working in teams, students built models predicting course evaluation scores and presented their final product in a poster session and research paper. To help increase variety in the final product, we kept the assignment open ended. An abbreviated version of the assignment is given below:

Data: Explain the data, including implications for the scope of inference.
Simple Linear Regression: Choose one quantitative explanatory variable and do a simple linear regression to predict average course evaluations.
Two Variable Comparisons: Explore relationships between each of the explanatory variables and average course evaluations as well as relationships between the explanatory variables.
Multiple Regression: Decide on a “best” model for predicting course evaluations and use it to obtain a predicted course rating for this course.
Conclusion: What have you learned about course ratings?

Teams focused on different aspects of the data and had different approaches to model selection, which promoted rich discussion during the poster session. One advantage of the poster session was that it required teams to reveal their answers simultaneously, eliminating the answer drift we tend to see in sequential presentations.

This data set also can be used in class discussions interspersed throughout the semester or at the end of a semester as review. Below, we have provided a series of questions that can be used as starting points for discussion. These questions do not require models that take into account the hierarchical structure of the data. For a list of discussion questions involving multilevel/hierarchical modeling of these data, see chapters 12, 13, and 16 in Data Analysis Using Regression and Multilevel/Hierarchical Models.

Discussion Questions

Data and Study Design

What does each observation in this data set represent? How are the observations sampled?
Are the observations independent of each other? Why, or why not?
Is this an observational study or an experiment? The original research question posed in the paper is whether beauty leads directly to the differences in course evaluations. Given the study design, is it possible to answer this question as it is phrased? If not, how would you rephrase the question?
In what analyses did the authors use the picture variables (pic_outfit, pic_color, pic_full_dept)? Should these variables be included in a model used to answer the main research question of the paper?

Course and Professor Evaluations

Describe the distributions of average course and professor evaluations. Is the distribution skewed? What does that tell you about how students rate courses? Is this what you expected to see? Why or why not?
How do average course and professor evaluations relate to each other? Do students tend to rate courses or professors more highly?

Professor and Class Characteristics

Explore bivariate relationships between various professor characteristics (rank, ethnicity, gender, language, age) as well as between course evaluations and each of these variables. Can you spot any trends?
Would you expect to see a relationship between class size and how highly the course is rated? If so, in which direction would you expect this relationship to be? Check if the data appear to support your expectation.
Are one-credit courses or multi-credit courses rated more highly? What reasoning do the authors give for this trend? Do you agree with their reasoning?

Beauty Scores

The paper states that students were asked to “use a 1 to 10 rating scale, […], to make their ratings independent of age, and to keep 5 in mind as an average.” Does it appear that the students followed the instructions?
Make scatterplots of beauty scores given by each student against the others. Do the students appear to agree on the beauty scores of professors?
Do male and female students tend to score similarly?
Do beauty scores appear to be dependent on whether the picture was black&white or in color, or whether the professor wore a formal outfit or not in the picture?
Fit a model predicting average course evaluations from average beauty scores and interpret the slope. Is average beauty score a statistically significant predictor? Does it appear to be a practically significant variable?
Should you include all beauty scores as explanatory variables in a model predicting course evaluations, a few of them, or only the average beauty score? Explain your reasoning and any selection criteria you might use.
The authors use unit normalized beauty scores in their analysis. They also create a composite standardized beauty rating for each instructor and they note that this reduces measurement error. Create this new composite standardized beauty rating variable and explain why this approach reduces measurement error.

Putting It All Together

Fit a multiple regression model predicting average course evaluations using an appropriate selection of the explanatory variables (excluding, at a minimum, average professor evaluation). Justify the model selection method you use.
Is beauty associated with differences in course evaluations? Is the association still present after accounting for other relevant variables? Do your findings agree with the results presented in the paper?
Use graphical diagnostic methods to check if conditions are met for this model. If conditions are not met, what are the implications?
Choose a model without any beauty variables to obtain a predicted course rating for this course and calculate the corresponding interval for this prediction. (Note that this question might require you to share some personal information with the students [e.g., age]. If you are feeling adventurous, you might consider allowing them to leave the beauty variable(s) in the model.)

This last question can lead to a discussion about generalizability—whether a model built on data from The University of Austin at Texas should be used for predictions at other institutions. Working with these data also gets students to think about the criteria they use when they fill out course evaluation forms; whether these variables are valid indicators of learning; and whether their own biases about looks, gender, race, and age are coming into play.

While some of the analyses presented in this article are beyond the scope of an introductory course, or even a second course in regression, a few simplifying assumptions make these data accessible to students at any level.