Christian Robert

The review of Anatyolev and Gospodinov (2011) is written by Brendan McCabe, professor in the economics, finance, and accounting department at the University of Liverpool Management School, United Kingdom. The other reviews are by Christian Robert.

Magical Mathematics: The Mathematical Ideas That Animate Great Magic Tricks

Persi Diaconis and Ron Graham

Hardcover: 258 pages
Publisher: Princeton University Press, first edition (October 2011)
Language: English
ISBN-13: 978-0691151649

“The two of us have been mixing entertainment with mathematics for most of our lives.” (Page xi)

When learning that Persi Diaconis and Ron Graham had co-authored a book on the mathematics of magic, I immediately asked Princeton University Press for a copy! Even though I am not at all interested in card tricks. Nor in juggling. (The title is a wee confusing [to a non-native speaker like me], as it sounds like focusing on the magics [sic] of mathematics, rather than the converse.)

Once the book arrived, I showed it to my wife, and she started reading it right away, going over the first chapter prior to returning it reluctantly. Later, on a plane trip between Phoenix and Minneapolis, I happened to sit next to a professional magician, The Amazing Hondo!, who started chatting with me about his work and some of his tricks. He knew about Persi as a magician, but was surprised he was equally famous among mathematicians and had not heard about the book. Hondo showed me a few (impressive) sleights of hand and explained a nice mathematical trick (based on creating apparent randomness while always extracting the same number of cards from the pile).

I have had a few other occurrences of how the book attracted the attention of non-magicians and/or non-mathematicians; this illustrates its appeal for a wide audience. Of course, once one starts reading the book, the attraction is increased. It is a very entertaining book, written at a fairly easy mathematical level. It is also beautiful, with wide margins, fancy (but readable) fonts, photographs, and graphs or tables in the margins.

“Both of our worlds have a dense social structure: thousands of players turning ideas over and over.” (Page xi)

The entertaining and cozy style of Mathematical Magics (oops, Magical Mathematics!) does not mean it is an easy read. First, conceptualizing the card manipulations requires a good analytic mind, if one does not have a deck of cards available. Second, the connections with mathematics involve several subfields, and not only combinatorics … de Bruijn sequences and graphs, the Mandelbrot set, Penrose tiling, Bayesian analysis for reversible Markov chains (Page 42), and the I Ching. … The last chapters are, however, less directly related to maths (even though Chapter 10 about great mathematical magicians includes connections with topology).

Interestingly (for us academics), the book mentions a (Banff ) BIRS 2004 workshop relating to magics via de Bruijn sequences and Gray codes, with the traditional picture in front of the (old) BIRS building. (Another item of information: IBM stands for International Brotherhood of Magicians!)

“We hope that our book will shine a friendly light on the corners of the world that are our homes.” (Page xii)

One of the complaints I share with my wife about Magical Mathematics is that some of the tricks are not explained in full enough detail. At least not for some non-native speakers like us. For instance, during my skiing break in the Alps, my nephew Paul and I tried the Gilbreath principle and could not make it work without forcing the perfect riffle-shuffle one card at a time. The sentence “the shuffle doesn’t have to be carefully done” (Page 63) set us on the wrong track. There were another few instances where I was confused, presumably again for being a non-native speaker.

Overall, this is a wonderful book, potentially enjoyable by a large range of individuals. (Precision: I read half of it flying over the beauty of sunsetted Greenland and the other half in a chalet next to the ski slopes. So I was in a particularly mellow spirit!) The order behind the apparent randomness of card tricks becomes clearer to the naïve reader like me. And the warmth and communal spirit of the magician community transpires through the last chapters. (Note there is a $1,000 reward posted within the book!)

Methods for Estimation and Inference in Modern Econometrics

Stanislav Anatolyev and Nikolay Gospodinov

Hardcover: 234 pages
Publisher: CRC Press, first edition (June 2011)
Language: English
ISBN-13: 978-1439838242

This book is a timely introduction to many of the latest techniques for estimation and inference in economic models. As usual when presenting material that is close to the cutting edge of research, decisions have to be made on the background assumed for the reader and on the level of technical detail to be included in the text. I think the authors got the balance just about right. There is sufficient detail, so the concepts and techniques are clearly explained and yet the reader is not overburdened with excessive minutiae. The authors also spend a lot of effort motivating and giving the intuition behind the various techniques involved.

The first section of the book (Chapter 1) gives a review of standard parametric and nonparametric inference. Topics include extremal estimators, generalized methods of moments, kernel and local polynomial regression, hypothesis tests, and bootstrapping. Models for both i.i.d. and dependent data are discussed.

The next section (chapters 2–4) deals with conditional moment models and covers material developed over the last 20 years or so. There are chapters on empirical likelihood, optimal instruments, and estimation of mis-specified models. The unifying feature is that many models in economics are not described by writing down a fully specified likelihood. Rather, they are partially specified using certain moment conditions only. The challenge is to use this partial information optimally for inference with respect to the parameters of interest. A slight oversight is, perhaps, that a large statistical literature on similar topics (estimating equations and quasi-likelihood) has not been mentioned, starting with Godambe (1960) and Durbin (1960) all the way through to Heyde (1997) and Sørensen (2012). This material has some interesting econometric applications when estimating continuous time diusions, as is popular in finance.

Section III (chapters 5 and 6) deals with higher-order asymptotics and asymptotics based on drifting sequences. The motivation for higher-order asymptotics is the usual one (i.e., the quality of approximations based on conventional central limit theorems is sometimes poor). The material here is pretty standard and uses asymptotic expansions for various moments and Edgeworth and saddle point expansions for sampling distributions.

Chapter 6 contains very interesting material on asymptotics based on parameters sequences that converge with sample size. One reason why conventional asymptotics sometimes gives poor results is that the limiting distribution of interesting estimators changes dramatically as certain parameters approach particular values, sometimes on the boundary of the parameter space. Perhaps the most well-known example is the discontinuity of the distribution of the OLS estimator of ρ in the AR(1) model

To get sampling distributions with nicer properties, models where

are considered. Many interesting variants of this drifting parameter idea are given with applications to weak instruments, regressions with extremely large numbers of regressors, change point models, and nearly nonstationary models like the aforementioned AR(1) model.

All in all, this book is well written and up to date. It would be suitable for graduate students and others looking for an accessible introduction to modern econometric methodology and thinking.

Further Reading

Godambe, V.P. 1960. An optimum property of regular maximum likelihood estimation. Ann. Math. Statist. 31:1208–1212.

Durbin, J. 1960. Estimation of parameters in time series regressions. J. Royal Statist. Soc. Series B 22:139–153.

Heyde, C.C. 1997. Quasi-likelihood and its applications. New York: Springer.

Sørensen, M. 2012. Estimating functions for diffusion type processes. In Kessler, Lindner, and Sørensen (Eds.) Statistical methods for stochastic differential equations, CRC Press.

Paradoxes in Scientific Inference

Mark Chang

Paperback: 291 pages
Publisher: CRC Press, first edition (June 2012)
Language: English
ISBN-13: 978-1466509863

The topic of scientific paradoxes is one of my primary interests, and I have learned a lot by looking at Lindley-Jeffreys and Savage-Dickey paradoxes. However, I did not recover a renewed sense of excitement when reading this book. The very first (and maybe the best) paradox with Paradoxes in Scientific Inference is that it is a book from the future! Indeed, its copyright year is 2013 (!), although I got it a few months ago. Unfortunately, I find the book very uneven and overall quite disappointing (even missing in its statistical foundations), especially given my initial level of excitement about the topic.

First, there is a (natural) tendency to turn everything into a paradox. Obviously, paraphrasing the hammer parable, when writing a book about paradoxes, everything looks like a paradox! This means bringing into the picture every paradox known to man and then some (i.e., things that are either un-paradoxical—Gödel’s incompleteness result—or irrelevant for a scientific book—the birthday paradox, which may be surprising but is far from being a paradox!).

Fermat’s theorem is also quoted as a paradox, even though there is nothing in the text indicating in which sense it is a paradox. (Or is it because it is simple to express, hard to prove?!)

Similarly, Brownian motion is considered a paradox, as “reconcil[ing] the paradox between two of the greatest theories of physics (…): thermodynamics and the kinetic theory of gases” (Page 51).

More worryingly, the author considers the MLE (maximum likelihood estimator) being biased to be a paradox (Page 117), while omitting the much more substantial paradox of the nonexistence of unbiased estimators for most parameterizations—which simply means unbiasedness is irrelevant, rather that MLE should not be considered, as hinted by the quote from Page 119 below. The author does not either allude to the even more puzzling paradox that a secondary MLE derived from the likelihood function associated with the distribution of a primary MLE may differ from the primary. (My favorite, see for instance Example 9.8.1 in Robert, 2001.)

“When the null hypothesis is rejected, the p-value is the probability of the type I error.” (Page 105)

“The p-value is the conditional probability given H₀.” (Page 106)

Second, the depth of the statistical analysis in the book is quite uneven. For instance, Simpson’s paradox is not analyzed from a statistical perspective, only reported as a fact. Sticking to statistics, take the discussion of Lindley’s (1957) paradox. The author seems to think the problem is with the different conclusions produced by the frequentist, likelihood, and Bayesian analyses (Page 122). This is the least interesting side of the picture. In my opinion, Lindley’s (or Lindley-Jeffreys’s) paradox is mainly about the lack of significance of Bayes factors based on improper priors.

Similarly, when the likelihood ratio test is introduced, the reference threshold is given as equal to one and no mention is later made of compensating for different degrees of freedom/against over-fitting.

The discussion about p-values is equally unsatisfactory. Witness the above quotes that (a) condition upon the rejection and (b) ignore the dependence of the p-value on a realized random variable.

“The peaks of the likelihood function indicate (on average) something other than the distribution associated with the drawn sample. As such, how can we say the likelihood is evidence supporting the distribution?” (Page 119)

The chapter on statistical controversies actually focuses on the opposition between frequentist, likelihood, and Bayesian paradigms. The author seems to have studied Mayo and Spanos’ Error and Inference (2010) to great lengths. He spends around 20 pages in Chapter 3 on this opposition and on the conditionality, sufficiency, and likelihood principles that were reunited by Birnbaum (1962) and deconstructed by Mayo in the above volume.

In my opinion, Chang makes a mess of describing the issues at stake in this debate and leaves the reader more bemused at the end than at the beginning of the chapter. For instance, the conditionality principle is confused with the p-value being computed conditional on the null (hypothesis) model (Page 110). Or with the selected experiment being unknown (Page 110). The likelihood function is considered a sufficient statistic (Page 137). The paradox of an absence of nontrivial sufficient statistics in all models but exponential families (the Pitman-Koopman lemma) is not mentioned. The fact that ancillary statistics bring information about the precision of a sufficient statistic is, however, presented as a paradox (Page 112). Having the same physical parameter θ is confused with having the same probability distribution indexed by θ, f(x; θ), which is definitely not the same thing (Page 115). The likelihood principle is further confused with the likelihood ratio test (Page 117) and maximum likelihood estimation (Page 117, witness the above quote). The dismissal of Mayo’s rejection of Birnbaum’s proof—a rejection I fail to understand—is not any clearer: “Her statement about the sufficient statistic under a mixed distribution (a fixed distribution) is irrelevant” (Page 138). Chang’s argument is that “given a sufficient statistic T, the distribution of x will vary as θ varies” (Page 138), which contradicts the very definition of sufficiency of a family of distributions.

“From a single observation x from a normal distribution with unknown mean µ and standard deviation σ it is possible to create a confidence interval on µ with finite length.” (Page 103)

One of the first paradoxes in the statistics chapter is the one endorsed by the above quote. I found it intriguing that this interval could be of the form x ± η|x| with η only depending on the confidence coverage. … Then I checked and saw that the confidence coverage was defined by default (i.e., the actual coverage is at least the nominal coverage), which is much less exciting (and much less paradoxical).

The author further claims several times to bring a unification of the frequentist and Bayesian perspectives, even though I fail to see how he did it. “Whether frequentist or Bayesian, concepts of probability are based on the collection of similar phenomena or experiments” (Page 63) does not bring a particularly clear answer. Similarly, the murky discussion of the Monty Hall dilemma does not characterize the distinction between frequentist and Bayesian reasoning (if anything, this is a frequentist setting).

A last illustration is the “paradox of posterior distributions” (Page 124), where Chang got it plain wrong about the sequential update of a prior distribution not being equal to the final posterior (see Section 1.4, Robert, 2001). He states that the former is [proportional to] the mixture

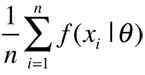
instead of the correct f (x₁, . . . , x_n |θ). A nice quote from Tony Hillerman is recycled from my book, but sadly misattributed:

“If you believe anything happens (…) for a reason, then samples may never be independent, else there would be no randomness. Just as T. Hilberman [sic] put it (Robert 1994): ‘From where we stand, the rain seems random. If we could stand somewhere else, we would see the order in it.’ ” (Page 140)

Most surprisingly, the book contains exercises in every chapter, whose purpose is lost on me. What is the point in asking students to “write an essay on the role of the Barber’s Paradox in developing modern set theory”? Or asking “how does the story of Achilles and the tortoise address the issues of the sum of infinite numbers of arbitrarily small numbers?” Culminating with the winner: “Can you think of any applications from what you have learned from this chapter?”

In conclusion, I feel the book is definitely overstretched in relation to its contents and missing too much in its foundations to be recommended. I also want to point out that, after I posted this review on my blog on November 23, 2012, the author replied on the same blog on December 26, 2012, in a very detailed way. The interested reader may thus confront my analysis against his reactions and draw one’s own conclusions.

Further Reading

Birnbaum, A. 1962. On the foundations of statistical inference. J. American Statist. Assoc. 57:269–306.

Lindley, D. 1957. A statistical paradox. Biometrika 44:187–192.

Mayo, D., and A. Spanos. 2010. Error and inference: Recent exchanges on experimental reasoning, reliability, and the objectivity and rationality of science. Cambridge: Cambridge University Press.

Robert, C. 2001. The Bayesian choice. 2nd ed. New York: Springer-Verlag.

In Pursuit of the Unknown: 17 Equations That Changed the World

Ian Stewart

Paperback: 352 pages
Publisher: Basic Books, first edition (March 2012)
Language: English
ISBN-13: 978-0465029730

I do not know if it is a coincidence or publishers are competing for the same audience. After reviewing The Universe in Zero Words: The Story of Mathematics as Told Through Equations in CHANCE 25(3), I noticed Ian Stewart’s 17 Equations That Changed the World and I bought a copy to check the differences between the books.

I am quite glad I did so, as I tremendously enjoyed this book, both for its style and its contents, as they were entertaining and highly informative. This does not come as a big surprise, given Stewart’s earlier books and their record; however, this new selection and discussion of equations are clearly superior to The Universe in Zero Words!

Maybe because it goes much further in its mathematical complexity, hence is more likely to appeal to the mathematically inclined (to borrow from my earlier review). For one thing, this book does not shy away from inserting mathematical formula and small proofs into the text, disregarding the risk of cutting off many halves of the audience. (I am aware that this is a mathematical absurdity!!!)

For another, 17 Equations That Changed the World uses the equation under display to extend the presentation much further than The Universe in Zero Words. It is also much more partisan (in an overall good way) in its interpretations and reflections about the world.

In opposition with The Universe in Zero Words, formulas are well presented, each character in the formula being explained in layman’s terms. (Once again, the printer could have used both better fonts and the LaTeX word processor. But this is a minor quibble!) Overall, 17 Equations That Changed the World makes for an enjoyable, serious, and thought-provoking read that I once again undertook mostly while in transit.

“Riemann, a brilliant mathematical talent (…), in a rush of blood to the brain, he also suggested ‘On the hypotheses which lie at the foundation of geometry.’ Gauss (…) naturally selected it for Riemann’s examination.” (Page 18)

The first equation in the book is Pythagoras’ Theorem, starting with the (indeed) “terrible pun about the squaw on the hippopotamus” (Page 3), not worth repeating here. It contains several proofs of the result, along with the remarkable fact that Babylonians were aware of the result in (circa?!) 7289 BC?! However, beyond historical connections, the chapter soon embarks upon a serious introduction to trigonometry. Then, Euclidean, non-Euclidean, and even Riemannian geometries.

The second chapter is about the invention of logarithms, with the fundamental feature of transforming products into sums, their applications in astronomy, the sliding rule (as of my high school years!), and the use of logarithms in the prediction of radioactive decay (with a completely superfluous paragraph on the Fukushima disaster!). As in The Universe in Zero Words, the use of e as the basis for the natural logarithms remains unexplained.

“The world view of humanity did not suddenly switch from religious to secular. It still has not done so completely and probably never will.” (Page 38)

The third chapter is based on the definition of the derivative. Unsurprisingly, the author being English implies that Isaac Newton gets the lion’s share in this formula, as well as in several other chapters. (Actually, to be fair, Gauss appears just as often in the book!) I find the above quote highly relevant for the long-term impact calculus had on Newton’s and Leibniz’s contemporaries’ view of the world. By introducing mathematical formulas behind the motion of planets, Newton and his predecessors—like Galileo and Descartes—“created the modern world” (Page 52). (The quote also reminds me of the atheistic reply of Molière’s Don Juan: “Je crois en deux et deux sont quatre, Sganarelle, et que quatre et quatre sont huit,” which is easier to put in a theater play than the formula for the derivative!) This chapter contains explanations on potential energy that are the clearest I have ever read.

Chapter 4 centers on Newton’s Law of Gravity in a sort of logical continuity with the previous chapter. I find this formula of gravitational attraction both fascinating and mysterious, and I have always been intrigued by how Newton (and others) came up with it. The chapter does a good job of explaining this derivation. It also covers Poincaré’s attack of the three body problem and the use of gravitational tubes to significantly improve the efficiency of space travel (with his costly mistake about chaos).

“Apparently, you can thread a hole through another hole, which is actually a hole in a third hole. This way lies madness.” (Page 95)

The next chapter and its equation i² = −1 are more traditional (and intersect with the list of The Universe in Zero Words), even though Stewart covers series expansions and complex exponential therein. Chapter 6 briefly dabbles in topology, thanks to Euler’s formula for polyhedra and its generalization. All the way through to knot theory, with Alexander’s and Jones’ polynomials.

“Fisher described his method as a comparison between two distinct hypotheses: the hypothesis that the data is significant at the stated level and the so-called null hypothesis that the results are due to chance.” (Page 122)

The only chapter truly connected with statistics is Chapter 7, providing the normal density as its motivating equation. It is not the best chapter of the book in my opinion as it contains a few imprecisions and hasty generalizations, the first one being to define the density as a probability of an event on the front page and again later (Page 115). And to have the normal distribution to supposedly apply in a large number of cases (Page 107), even though this is moderated in the following pages.

What is interesting though is the drift from Pascal, Gauss, Legendre, and Laplace toward Quetelet, Galton, and then Fisher, the Pearsons, and Neyman, missing Gosset. Stewart mentions Galton’s involvement in eugenics, but omits the similar implication of Fisher and Pearson as author in and editor of the Annals of Eugenics.

The chapter confuses to some extent probability and statistics, calling the stabilization of the frequencies a “statistical pattern” when it simply is the Law of Large Numbers. (Although it may be that, for mathematicians, statistics can be reduced to this law.)

The above quote reflects some of the imprecision transmitted by the author about testing. The fact that “the data is significant at the stated level” α means it does not support the null hypothesis, not that the alternative hypothesis is true. Stewart states as much in the following sentence, stressing that rejecting the null “provides evidence against the null not being significant” (Page 123), but I find it unfortunate that the tool (checking that the data is significant at level α, which means checking a certain statistic is larger than a given quantile) is confused that way with the goal (deciding about a parameter being different from zero). He further subsumes his first mistake by asserting that “the default distribution for the null hypothesis is normal: the bell curve” (Page 123). This unifies the chapter, of course, and there is some sensible justification for this shortcut, namely that the null hypothesis is the hypothesis for which you need to specify the distribution of the data, but this is nonetheless awkward.

Rather interestingly, the chapter concludes with a section on another bell curve, namely the highly controversial book by Herrnstein and Murray arguing for racial differences in the distribution(s) of the IQ. This thesis was deconstructed by statisticians in Devlin et al.’s Intelligence, Genes, and Success, but 17 Equations sums up the main theme—the huge limitations of the IQ as a measure of intelligence.

Neither Bayes’s formula nor Thomas Bayes are to be found in the book, just as in The Universe in Zero Words. (Jeffreys is one of the two Bayesians mentioned in 17 Equations That Changed the World, but in his quality of a seismologist [see below]).

“If you placed your finger at that point, the two halves of the string would still be able to vibrate in the sin 2x pattern, but not in the sin x one. This explains the Pythagorean discovery that a string half as long produced a note one octave higher.” (Page 143)

The following chapters are all about physics: the wave equation, Fourier’s transform and the heat equation, Navier-Stokes’ equation(s), Maxwell’s equation(s)—as in The Universe in Zero Words, the second law of thermodynamics, E = mc² (of course!), and Schrödinger’s equation. I won’t go so much into details for those chapters, even though they are remarkably written. For instance, the chapter on waves made me understand the notion of harmonics in a much more intuitive and lasting way than previous readings. (Chapter 8 also mentions the “English mathematician Harold Jeffreys,” while Jeffreys was primarily a geophysicist. He also was a Bayesian statistician with major impact on the field, his Theory of Probability arguably being the first modern Bayesian book. Interestingly, Jeffreys also was the first one to find approximations to the Schrödinger’s equation, however he is not mentioned in this later chapter.)

Chapter 9 mentions the heat equation, but is truly about Fourier’s transform, which Fourier uses as a tool and later became a universal technique. It also covers Lebesgue’s integration theory, wavelets, and JPEG compression.
Chapter 10 on Navier-Stokes’ equation also mentions climate sciences, where it takes a (reasonable) stand. Chapter 11 on Maxwell’s equations is a short introduction to electromagnetism, with radio the obvious illustration. (Maybe not the best chapter in the book.)

“To understand the Carnot cycle, it is important to distinguish between heat and temperature (…) In a sense, heat is a bit like potential energy.” (Page 202)

Chapter 12 discusses thermodynamics, not through the traditional pV = RT, but rather with the second law of the increase of entropy (which is precisely an inequation, as remarked by Stewart in his notes). It explains this elusive notion (entropy) via the Carnot cycle and its transform into a perfect rectangle, one of the most efficient descriptions I have seen on the topic! Brownian motion (to re-enter the scene later!) is mentioned as being a major step in accepting Botlzmann’s kinetic interpretation. (The final discussion about the connections between time-reversibility and entropy gets a bit confusing, especially as it concentrates on scrambled eggs!)

Chapter 13 is covering the (almost compulsory) E = mc², explaining some of Einstein’s inputs in a rather satisfactory manner, covering the Michelson-Morlay experiment (which we use as a benchmark in our incoming new edition of Bayesian Core) making links with Galileo, Maxwell, and non-Euclidean geometries since it introduces the Minkowski space-time representation. It also debunks a few myths about Einstein, and then moves to highly interesting issues like space warped by gravity, the precession of Mercury (with Le Verrier’s theoretical “discovery” of Vulcan), and cosmology. It even goes as far as spending a few pages on the current theories offered for modernizing the cosmological paradigm. (The chapter mentions the now resolved Gran Sasso controversy about neutrinos travelling “faster than light.” Page 226.)

“The notion of information has escaped from electronic engineering and invaded many areas of science, both as a metaphor and as a technical concept.” (Page 281)

I am afraid I will skip describing Chapter 14 about quantum theory, as I find it spends too much time on Schrödinger’s cat, which makes it sound like the hype vocabulary so readily adopted by postmodernists, without any understanding of the physics behind it. And botching its explanation of the quantum computer. (Even though I liked Stephen Hawking’s quote of the multiverse formalism as “conditional probabilities,” Page 262!)

Chapter 15 gets back to entropy by being centered on Shannon’s information formula. Maybe because I wrote one of my master projects on error-correcting codes, I was not very excited by this chapter. Even though Stewart ends up with DNA and its information content, the impact of Shannon’s definition does not seem of the same scale as, say, Newton’s Law of Gravity. It is also fraught with the same danger as the previous notion, namely to use this notion inappropriately. Not so coincidentally, Edwin Jaynes makes a natural appearance in this chapter (as an “American physicist,” Page 282, despite having written Probability Theory, dedicated to Harold Jeffreys, and being the charismatic father of the maximum entropy principle). Stewart signals that Jaynes stressed the inappropriateness of assimilating entropy with missing information in every context.

Chapter 16 deals with another hype theory, namely chaos theory, by picking the logistic chaotic equation (or map)

which exhibits unpredictable patterns while being completely deterministic and that I used to play with when I got my first PC. This chapter does not get much farther, even though it mentions Poincaré again, as well as Smale, Arnold, and, obviously, Lorenz. While we do not escape the compulsory butterfly story—which, incidentally, originated from Ray Bradbury and not from Lorenz—we at least avoid being dragged into the Mandelbrot set, as would have been the case 20 years ago. However, the chapter fails to explain in which sense chaos theory is more than a descriptive device, except for a very short final paragraph.

“How did the biggest financial train wreck in human history come about? Arguably, one contributor was a mathematical equation.” Page 298)

As in The Universe in Zero Words, the last chapter is about Black and Scholes’ formula, again maybe inevitably given its presupposed role in “ever more complex financial instruments, the turbulent stock market of the 1990s, the 2008–9 financial crisis, and the ongoing economic slump” (Page 295)?

Despite its moralizing tone, the chapter does a reasonable job of explaining the mechanisms of derivatives, starting with the Dojima rice future market in the Edo era (incidentally, I found that the description on pages 298–299 parallels rather closely the Wikipedia article on the Dojima Rice Exchange!). It also covers Bachelier’s precursor work on the (potential) connection between stock markets and the Brownian motion introduced earlier. Opening the gates for blaming the “bell curve” on not predicting “black swans” (with Stewart referencing Taleb’s 2007 book on Page 301 and mostly rephrasing Taleb’s leading theme about fat tails in the following pages). The following reference is a talk given by Mary Poovey at the International Congress of Mathematicians in Beijing in 2002 pointing out the dangers of the virtual money created by financial markets, especially derivatives: I presume many prophetic warnings of that kind could have served the same purposed, as fulfilled prophecies are rather easily found a posteriori.

“The Black-Scholes equation is also based on the traditional assumptions of classical mathematical economics: perfect information, perfect rationality, market equilibrium, the law of supply and demand (…) Yet they lack empirical support.” (Page 310)

What I find most interesting about this last chapter is that it is about a formula that did not “work,” in opposition to the previous 16 formulas, although it equally affected the world, if possibly (and hopefully) for a short time. Since it is more or less the conclusive chapter, it gives a rather lukewarm feeling about the limitations of mathematical formulas: As bankers blindly trusted this imperfect representation of stock markets, they crashed the world’s economies. This turning the Black and Scholes formula into the main scapegoat sounds a wee simplistic, especially given the more subtle analyses published after the crisis. (I am not even sure that the Black-Scholes equations were ever adopted by their users as a way to represent reality, but rather as a convention for setting up prices.) The Universe in Zero Words was much more cautious (too cautious) about what caused the crisis and how much the Black-Scholes equation was to blame. Maybe the most popular chapter in the book, to judge from reviews, but rather off the mark in my opinion.

Interestingly, the final page of the book (Page 320) is a skeptical musing about the grandiose theories advanced by Stephen Wolfram in A New Kind of Science, namely that cellular automata should overtake traditional mathematical equations. Stewart does not “find this argument terribly convincing,” and neither do I.

Let me conclude with an anecdote about equations. When I took part in a radio emission about Bayes’ formula, expressed via events A and B, the presenter asked me to draw a comparison with Newton’s Law about the meaning of the symbols, hoping for a parallel in the former to the mass and distances in the latter. This simply shows that what we academics take for granted is often out of reach for the masses and requires pages of explanation we would deem superfluous. If only for this reason, 17 Equations that Changed the World is a wonderful book.

Further Reading

Devlin, B., S.E. Fienberg, D.P. Resnick, and K. Roeder. 1997. Intelligence, Genes, and Success: Scientists respond to the bell curve. New York: Springer-Verlag.

Herrnstein, R.J., and C. Murray. 1994. The bell curve. New York: The Free Press.

Jaynes, E. 2003. Probability theory. Cambridge: Cambridge University Press.

Jeffreys, H. 1939. Theory of probability. Oxford: The Clarendon Press.

Taleb, N.N. 2007. The black swan: The impact of the highly improbable. New York: Random House.

Wolfram, S. 2002. A New Kind of Science. Champaign: Wolfram Media.

Guesstimation: Solving the World’s Problems on the Back of a Cocktail Napkin

Lawrence Weinstein and John A. Adam

Paperback: 320 pages
Publisher: Princeton University Press (first edition, April 2008)
Language: English
ISBN-13: 978-0691129495

 

 

 

 

 

 

~ and ~

 

Guesstimation 2.0: Solving Today’s Problems on the Back of a Napkin

Lawrence Weinstein

Paperback: 384 pages
Publisher: Princeton University Press (first edition, October 2012)
Language: English
ISBN-13: 978-0691150802

When I received the book Guesstimation 2.0 for review, I decided to purchase the first (2008) volume, Guesstimation, so this is a joint and comparative review of these books.

The title may be deemed to be misleading for (unsuspecting) statisticians as, on the one hand, the books do not deal at all with estimation in our sense, but with approximation to the right order of magnitude of an unknown quantity. It is thus closer to Paulos’ Innumeracy than to Statistics for Dummies, in that it tries to induce people to take the extra step of evaluating, even roughly, numerical amounts (rather than shying away from it or, worse, trusting the experts!). For instance, how much area could we cover with the pizza boxes Americans use every year? About the area of New York City. (On the other hand, because Guesstimation forces the reader to quantify ones guesses about a certain quantity, it has the flavor of prior elicitation and thus this guesstimation could well pass for prior estimation!)

In about 80 questions, Lawrence Weinstein (along with John A. Adam in Guesstimation) explains how to roughly “estimate” (i.e., guess) quantities that seem beyond a layman’s reach. Not all questions are interesting. In fact, I would argue they are mostly uninteresting per se (e.g., What is the surface of toilet paper used in the U.S.A. over one year? How much could a 1km meteorite impacting the Earth change the length of the day? How many cosmic rays would have passed through a 30 million-year-old bacterium?), as well as very much centered on U.S. idiosyncrasies (i.e., money, food, cars, and cataclysms). And some clearly require more background in physics or mechanics than you could expect from the layman (e.g., the energy of the Sun or of a photon, P = mgh/t, L = mvr (angular momentum), neutrinoenergy depletion, microwave wavelength, etc. At least the book does not shy away from formulas!)

So, neither Guesstimation nor Guesstimation 2.0 makes for a good bedtime read or even a pleasant linear read. Except between two metro stations. (Or when flying to Des Moines next to a drunk woman, as it happened to me …) However, the books provide a large source of diverse examples that is useful when you teach your kids about sizes and magnitudes (it took me a while to convince my daughter that 1 cubic meter was the same as 1000 liters!); your students about quick and dirty computing; or anyone about their ability to look critically at figures provided by the news, the local journal, or the global politician. Or when you suddenly wonder about the energy produced by a Sun made of … gerbils! (This is Problem 8.5 in Guesstimation, and the answer is as mind boggling as the question!)

To help with this reasoning and the recovery of (magnitude) numeracy, Weinstein added in Guesstimation 2.0 an appendix called “Pegs to Hang On,” where he lists equivalent objects for a range of lengths, weights, etc. (The equivalent can be found in Guesstimation.)

The books both start with a similar section on how to make crude evaluations by bounding the quantity and taking the geometric mean. I also like the way Weinstein battles for using metric units and powers of 10 in calculation and joins us in fighting against extra digits, claiming they are lies, not precision, which is true!

A few problems in Guesstimation 2.0 irked me, including all related to recycling, because they concentrated on the monetary gain provided by recycling a bottle, a can, etc., versus the time required for an individual to dump this object in the right bin: not the most constructive approach to recycling (see instead David McKay’s Sustainable Energy Without the Hot Air). The same is true for the landfill question in Guesstimation: the volume of trash produced by Americans over 100 years may well fit in a 100 m high hill over 106 square meters, but landfills are definitely not the solution to garbage production!

There are also one or two probability-related problems. For instance, the one about getting a baseball inside one’s beer glass during a game. Weinstein goes from the probability of getting one foul ball being 3 10−4 to the probability of getting one of the 40 foul balls during one game equal to 10−2 without the beginning of an explanation. (This is true, but how does he get there?!) By the way, it seems question 7.10 did not make it to Guesstimation 2.0, as it reads as a quick intro to angular momentum—a recap usually found at the start of a chapter.

And what about a comparison between Guesstimation 2.0 and Guesstimation? Well, as you can guess (!), they are quite similar. Overall, I would tend to find Guesstimation more engaging and funnier (like the joke about advising against storing a cubic meter of uranium under your kitchen table!), as well as more diverse in its choice of questions (with a section on risk (e.g., computing that smoking a cigarette costs you in life expectancy the time it takes to smoke it, similar to the evaluation that driving a car costs you in working hours the time you are driving it). But, again, these books are not primarily designed for linear reading, so they both come as a good resource for numeracy tests and quizzes, Guesstimation 2.0 simply adding to the pool like an extra box of Trivial Pursuit cards …

Note that, in addition to the 80 questions processed in Guesstimation, the book concludes with a list of 30 unanswered questions. (I liked the one about the potential energy of a raindrop in a cloud, as it reminded me of a recent entry in Le Monde science leaflet about the strategy mosquitoes implement to avoid being flattened by those monstrous drops!)

Further Reading

Mackay, D. 2009.Sustainable Energy Without the Hot Air. UIT Cambridge.

Paulo, J.A. 1988. Innumeracy: Mathematical illiteracy and its consequences. New York: Hill and Wang.

Back to Top

[/restrict]