Michael Orkin

Advances in technology and high revenue potential have led to a proliferation of online gaming, particularly fantasy sports such as the games offered by FanDuel and DraftKings. Due to relaxation of federal gaming laws, it is usually up to the states to determine what is legal and what is not. As a result, some states allow more online gambling than others, with the decision typically based on whether games are skill-based or have a “material degree of chance.”

For example, in New York, a “contest of chance” (i.e., illegal gambling game) is defined as “any contest, game, gaming scheme, or gaming device in which the outcome depends in a material degree upon any element of chance, notwithstanding that skill of the contestants may also be a factor therein.” (There are efforts underway in New York to modify its rule by changing “material degree” to “predominantly,” although this has not happened yet.)

The material degree of chance rule has kept some states from legalizing sports betting, even fantasy sports, causing issues for the app industry (legal in some states, illegal in others), where much of this activity takes place.

This rule is somewhat political. All games, even those that are skill-based, have a degree of chance (if two golfers of equal skill play each other, the winner is largely determined by chance). This potentially allows regulators to select the legality of whatever online games they want. Fortunately for the industry, the tax revenues from gambling apps—fantasy sports alone is now a multi-billion-dollar industry—have caused regulators to work with developers, and many states now allow fantasy sports gaming.

Until now, determination of chance or skill has largely been done by negotiations between attorneys and regulators. Recently, statisticians have become involved, usually hired as consultants by attorneys for game companies that are arguing for legality of their games. The definition of material degree of chance has been questioned, sometimes successfully.

Analyzing a fantasy-like gaming app to determine whether it offered games of skill or games of chance, based on a statistical argument, led to the conclusion that the games were skill-based. The method employed for this analysis can also be used to show that other types of games are skill-based.

The Chance-Skill Spectrum

It has been customary to discuss the skill level in games by using a “chance-skill scale,” where games of pure chance, like craps and roulette, are at one end; games of skill, like golf and bowling, are at the other end; and games with both chance and skill, like blackjack and poker, are in the middle (when golf and bowling are called games of skill, the actual games are referred to, not betting on them).

I testified in a case a few years ago and was asked in court to draw the chance-skill spectrum on a whiteboard. In fact, though, the spectrum does not answer the question of whether a particular game has a “material degree” of chance. Deciding where to draw the line between chance and skill does not work if all games have an element of chance and if there is no clear way to rank games according to their skill level. (Does blackjack involve more skill than poker? Do fantasy sports involve more skill than blackjack? If so, why?)

The New York definition of material degree of chance could also be interpreted to mean that all games have a material degree of chance, and thus is useless. There is a simple way to distinguish between games that are skill-based and those that have a material degree of chance that does not involve a chance-skill scale.

Games like craps, roulette, and lotteries are easy to categorize as games of pure chance, because the player is betting against random numbers. Although someone playing one of these games can get lucky from time to time, the law of averages ensures that a gambler’s win percentage in repeated play of a game like this will converge to “average,” and luck will disappear.

Blackjack is a skill-based game, as popularized by Ed Thorp’s book, Beat the Dealer, originally published in 1962 and still in print more than half a century later, as well as numerous succeeding books written by a variety of authors. If you take the time to learn a card-counting strategy, as taught in these books, you can win against the casino under good playing conditions. This has been verified by thousands of blackjack players over the years. It does not make much sense to categorize blackjack with roulette and craps as having a material degree of chance, yet this is sometimes done. And what about fantasy sports wagering?

Sports Wagering, Fantasy and Otherwise

In traditional sports betting, the gambler bets on the outcome of a game, with odds or point spreads included to help the casino ensure a profit. In the past few years, fantasy sports gaming has proliferated due to online technology. In fantasy wagering, you put together your own team, based on actual players, and earn points depending on how your team performs during the season. Fantasy sports companies have successfully argued that skill is needed to put together a team for a sport and have generally been granted approval for their apps.

Other sports wagering games, such as the one discussed here, have been developed in which, instead of betting on the outcomes of games (traditionally forbidden), one bets on the outcomes of situations within a game, such as who will score the next touchdown, or who will make the next three-point shot. These wagers may involve skill.

A statistical approach to the chance or skill determination would be to analyze betting data to see if there are consistent winners—gamblers who do significantly better in repeated play than chance allows. If there are such players, there is a skill element that overrides chance and demonstrates that these are skill-based games.

Definitions

• Luck means doing better (or worse) than average due solely to chance. For example, when guessing the number of times that heads will appear in coin tossing, the average success rate is 50%. This uses “luck” interchangeably with “chance.”

• A skilled player is someone who has a significantly higher win percentage than luck allows.

• An unskilled player is someone whose betting strategy is equivalent to random guessing, such as tossing a coin to decide what to do. Note: In a game setting where two players are pitted against each other, unskilled players might play against skilled players and lose significantly more often than chance allows. In the current setting, players are betting against the “house” and so, unless a player has found a way to lose on purpose, an unskilled player will have win-loss results within the range of chance. This was borne out in the data.

• A game is skill-based if it has skilled players.

• A game has a material degree of chance if there are no skilled players; that is, the win percentages of all players are within the range that chance allows.

Whether a gambler is skilled is determined by hypothesis testing. Similar to the legal principle of “innocent until proven guilty,” this starts by assuming that a player is unskilled (null hypothesis). The unskilled or “chance” hypothesis is rejected with the conclusion that a player is skilled if there is a very low probability (p-value) that an unskilled player could achieve the player’s observed results due only to luck.

In analyzing betting data for this project, numerous players showed performance that was significantly better than what an unskilled player could accomplish, even if the unskilled player was lucky. Note: In two player matchups, in which the players are pitted against each other rather than against the casino, it would be assumed that all players have equal skill until proven otherwise (statistically). An analysis of this type in a different setting yielded similar results.

An analysis like this requires testing many hypotheses—one for each player in the database. Each player has their own p-value, determined by the player’s win-loss record. To use classic statistics rather than just p-values requires setting an appropriately low significance level for multiple tests. Note: Rejecting the null hypothesis in favor of skill requires being sensitive to other plausible alternatives, like cheating, that could also allow a player to have a significantly higher win percentage than luck allows.

Discussions with the game developer and the relatively large number of winners found no evidence of cheating in the current analysis. (It would be interesting to do a more in-depth study of cheating, but that is beyond the scope of this work.)

Analysis

The wager analyzed here is similar to a two-team parlay in ordinary sports betting, in which the gambler has to pick the winners of two teams (in these games, two situations) to win the bet. For example, if you pick Kansas City and Green Bay in a two-team parlay in ordinary sports betting, you win your bet only if both teams win their (separate) games. If one team wins and one team loses, or if both teams lose, you lose your bet.

Although skilled players usually make a profit, this analysis is based on win percentages only. As is the case with any gambling game, a player can have a skill-based strategy and still lose money. For example, in traditional sports betting, a four-team parlay offers 10 to 1 payoff odds. The chance of winning such a bet for someone who is guessing equals (½)⁴ = 0.0625. This gives the casino a 31.25% advantage (expected winnings = 10*.0625 -1*.9375 = -.3125). In other words, the unskilled player will lose 31.25 cents per dollar bet in repeated play.

A skilled player who wins a four-team parlay 8% of the time is doing better than the unskilled rate of 6.25%, but will still lose 12 cents per dollar bet in repeated play. In addition, any player who achieves a high success rate might use poor money management, resulting in a net loss even though they are a skilled bettor.

Data

This analysis involved player data for “fantasy” wagering in NBA, NFL, Soccer EU, and other sports leagues for the time period 2018 through 2019, using a database with 11,694 players with a total of 343,458 contest entries. Having a reasonable n for significance testing meant reducing this data set to the 1,460 players who made at least 20 wagers each.

The analysis was across sports: fantasy sports contests similar to parlay bets, but in which the wagers were not based on the outcomes of games themselves but on events taking place within games. In this format, you make predictions for the outcomes of multiple events, where each outcome is either win or lose, and have to predict all the outcomes correctly to win. This discussion looks at two-way parlays only.

Since there is a 50% chance that random guesser will make a correct prediction for one situation with two possible outcomes (like tossing a coin), the chance of making two correct picks in a two-way parlay equals ½ x ½ = ¼. In addition, random guessing, like tossing a coin to decide who to pick, creates independent events.

In repeated play, by the law of averages, someone with no skill playing two-way parlays will win about ¼ of the time. A win percentage above 25% indicates that the player is either lucky or even doing better than luck. By the law of averages, the fraction of wins by an unskilled player converges to .25 as the number of bets gets large. In the long run, luck disappears, and all random guessers become “average.” Skilled players, on the other hand, maintain their winning ways and get a higher win percentage than is possible through chance alone.

The Binomial Model

In two-way parlay betting, the probability that an unskilled player using random guessing will obtain k wins in n bets has a binomial distribution, X, with parameters n, ¼. Using the binomial model, the probability that someone will get a high number of wins in repeated play can be determined, with a formula of the form P(X ≥ k). If this probability, known as a p-value, is extremely low, luck can be ruled out and it can be concluded that the player is skilled (or there is some other plausible reason for the high success rate). This analysis used Excel and the Excel function “binom.dist,” so that with n wagers, the probability of k or more wins would be computed by P(X ≥ k) = 1-binom.dist(k-1,n,.25,true).

Significance Level

In classic statistics, the cutoff point between luck and skill is called the “significance level” of the test and is traditionally equal to 0.05: A p-value would have to be lower than 0.05 to reject luck in favor of skilled play. However, if there are many players, the significance level has to be adjusted, since some players could have p-values of less than 0.05 due to chance. For example, if 50 players were guessing at random, you would expect two or three to have p-values of less than 0.05.

As mentioned earlier, there were more than 10,000 gamblers in the study, 1,460 of whom made 20 or more wagers. This means 1,460 hypothesis tests and resulting p-values. Of these players, 50—or 3.4%—had p-values <.000034, which was the cutoff point for significance due to the large number of players. The remaining 1,410 players had p-values > .000034, within the range of chance. None of the players did worse than chance allows, according to a reasonable significance level (the lowest p-value on the losing end was p = .012). (We used the Bonferroni correction for multiple comparisons with with 1460 comparisons and original significance level equal .05 to yield new significance level = .05/1460 = 0.000034.)

Since the players were playing against the house, this was to be expected.

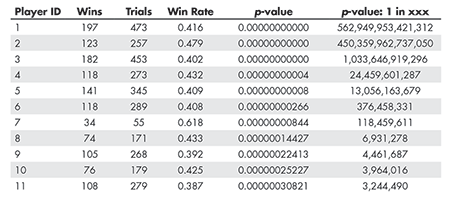
The lowest p-value was for a player who had 197 wins in 473 wagers, for a win rate of 0.42, as opposed to an unskilled player’s long-term win percentage of 0.25. This player’s p-value, based on win rate, was less than 1 in 562 trillion, a p-value so low that it is essentially impossible for an unskilled player to get this result by luck. The expected value, E, of a geometric random variable, which indicates time to the first success, equals 1/p. In this case, E > 562 trillion.

If everyone on Earth (7 billion people) were to enter 473 two-way contests every day, 365 days per year, and toss coins to make picks, it would take an average of > 220 years until someone gets at least 197 wins in 473 two-way parlays just by getting lucky. Practically speaking, it is not going to happen. This would be like putting monkeys in front of typewriters and hoping that, given enough time, they will randomly write the works of Shakespeare.

As the table shows, 11 gamblers had p-values less than 1 in 1 million; that is, the chance is less than 1 in a million that a random guesser would do this well just due to luck. An additional 29 players had p-values of less than 1 in 100,000. These 40 players are all skilled. Their success rates are considerably higher than an unskilled player could achieved—even a lucky one, and even with so many players.

Combined Results

As shown, the unskilled probability of success for a two-way parlay equals ¼. There were other parlay bets as well. For example, in a three-way parlay, a player has to get three out of three picks correct to win their bet. A four-way parlay requires getting four out of four correct, etc. Each parlay category can be analyzed using the binomial model in the same way that the two-way parlays were analyzed. Doing this found numerous players in every parlay category with low p-values.

What if the goal is to combine the results of the different parlay categories to get overall win percentages for the players? Since binomial success probabilities for unskilled players are different for different parlay bet types, the results cannot be combined directly. Instead, the binomial probabilities can be approximated by the normal distribution whenever the number of trials is large enough—specifically, whenever n*p > 5 and n*(1 – p) > 5, where n = number of plays and p = binomial (parlay) success probability for an unskilled player.

This, coupled with the fact that the sum of independent normal distributions has a normal distribution, with mean equal to the sum of individual means and variance equal to the sum of the variances, makes it possible to analyze a player’s combined results for different contest types (independence due to null hypothesis of random guessing).

Doing this found numerous players who were skillful across contest types and whose p-values (using the normal distribution) were small enough to rule out chance (this is not part of the analysis above).

Profit

Although most of the skilled players profited from their play, a few lost money even though they had extremely low p-values. For example, one player lost $2,180.80 over the course of 1,434 plays, with an average loss of $1.52 per play. It may seem paradoxical for a skilled player to lose money, but it happens. It could be due to a very unfavorable odds structure (only wins and losses are discussed here), or a player could be skilled at winning parlays but use poor money management—any player, skilled or not, who bets their entire bankroll on every play will soon go broke.

Conclusion

A skilled player is defined as someone whose win percentage is significantly higher than chance allows. A skill-based game is one that has at least one skilled player. An unskilled player is a gambler whose betting strategy is equivalent to that of a random guesser. A game with a material degree of chance is one with no skilled players. A statistical analysis of two-way sports parlay wagers showed that many players were skilled.

Although an unskilled player can get lucky and have a higher than average win percentage, in repeated play, luck disappears and, by the law of averages, unskilled players revert to average, which is a 25% win probability in the case of two-way parlays. Only a skilled player who does better than luck will have a win percentage significantly higher than 25%.

This analysis involved computing p-values for the win percentages of numerous players. Because of the many skilled players discovered in the course of this analysis, the results showed that the games being analyzed are skill-based activities that do not involve a material degree of chance.

About the Author

Mike Orkin is a mathematics professor at Berkeley City College and professor of statistics, Emeritus, at California State University, East Bay. He is a consultant and a nationally known authority on probability and gambling games. He has appeared on numerous TV and radio shows, including CBS Evening News, NBC Bay Area, ESPN, CNN, Fox News, and NBC’s Dateline. He earned his PhD in statistics from the University of California, Berkeley. Mike is also on the Board of Trustees of Lincoln University in Oakland, California.

Back to Top