Leonard M. Wapner

When some systems are stuck in a dangerous impasse, randomness and only randomness can unlock them and set them free.
—Nassim Nicholas Taleb

Negotiation deadlocks in business, politics, and social interactions can be costly in more ways than one. An arbitration scheme developed by Nobel Prize-winning mathematician John Nash provides a way to break budget impasses and similar negotiation deadlocks such as those leading to the U.S. government shutdowns in 2018–19. The scheme is elegant, fair, and efficient for all parties, providing a unique resolution. Surprisingly, it also relies on a randomizing device, such as the toss of a coin or a random lottery.

Flip Decisions

How do you celebrate June 1—U.S. National Flip a Coin Day? You don’t, and neither does anyone else. But there is something to be said for “letting the dime decide” when people are unable to make a decision.

At an early age, children learn that “flipping for it” affords a quick, simple, and fair way to settle disputes. By letting chance decide, they can’t blame themselves or the others for the outcome. The tradition is believed to date back to Julius Caesar, who would toss a coin to make difficult decisions. “Heads” was associated with the side of the coin showing his image. Throughout history, there have been many notable flip decisions.

· In 1845, a coin toss gave Portland, Oregon, its name over the alternative “Boston.”

· Wilbur and Orville Wright tossed a coin in 1903 to determine which of the two would pilot the first flight. Wilbur won the toss, but crashed on his attempt. Orville later made the first successful flight.

· A coin toss on February 3, 1959 (“The Day the Music Died”), gave Latin star Ritchie Valens the last seat on the ill-fated flight from Mason City, Iowa, to Fargo, North Dakota. The plane crashed, killing Valens, Buddy Holly, J.P. “The Big Bopper” Richardson, and the pilot, Roger Peterson.

· A coin toss in 1969 determined the owner of what became Triple Crown winner Secretariat, arguably the greatest racehorse of all time. Penny Chenery of Meadow Stable, a Thoroughbred racing operation and horse breeding business at The Meadow in Caroline County, Virginia, lost the toss, leaving her with the yet-unborn foal that she called Big Red but whose official name was Secretariat.

· In the Donald Duck episode “Flip Decision,” Professor Batty converts Donald to the pseudo-philosophy of flipism, where all life’s major decisions are made by the flip of a coin. The Great Society of Flippists proclaims, “Life is but a gamble! Let flipism chart your ramble!”

Coin tossing is almost always associated with an inability to decide caused by indifference or conflicting preferences. Beyond this, randomization in the form of a coin toss or lottery may provide the only means of achieving a fair and efficient resolution as defined by Nash.

The Potential Cost of a Budget Impasse

The U.S. Antideficiency Act, enacted in 1870 and amended over the years, is intended to prevent government expenditures in excess of available funds. As a consequence, a government shutdown occurs when Congress and the president fail to meet the associated deadline. Such an impasse occurred most recently in February 2019 when the U.S. Senate failed to get the required 60% of its members to pass a government funding law.

In the January 2018 shutdown, Democrats insisted the bill include provisions, including a path to citizenship, to protect roughly 2 million undocumented young immigrants brought to the United States illegally, known as DREAMers. United States President Donald Trump and Republican senators rejected this, favoring instead funding for stronger border protection, including construction of a wall on the United States/Mexico border.

These options were rejected by Democrats. At the time, Republicans controlled 51 of the 100 Senate seats. In a highly polarized atmosphere with senators voting close to party lines, a vote to advance the proposed bill split, falling far short of the 60% supermajority required to pass. A brief government shutdown followed. The deadlock was caused by legitimate differences combined with polarization and political brinksmanship, with both parties prepared to go over the cliff into a government shutdown if no agreement was reached.

We recognize this as classical “chicken,” the theoretical dilemma game arising in the behavioral sciences. The 2019 shutdown created a similar impasse and associated shutdown.

Shutting down the government costs U.S. taxpayers billions of dollars each week the shutdown is in effect. Federal workers may be furloughed or have their pay delayed. Government services are curtailed. Additional costs are associated with lost productivity and in preparing for the possibility of future shutdowns.

Neither political party wants such an outcome, but such is the nature of brinkmanship, politics, and the game of chicken.

A Nash Model of a Simple Arbitration

Mathematically, resolving such a deadlock can be thought of as negotiating a settlement in a non-zero-sum game. This is best illustrated with a highly simplified model of such a negotiation and then applying the Nash arbitration scheme to arrive at a settlement.

Assume Democrats and Republicans are deadlocked over a negotiation involving three possible settlement outcomes. Democrats prefer outcome A: assistance for DREAMers, over outcome B: building a border wall. Republicans prefer outcome B over outcome A. Both parties prefer either outcome to outcome SQ: the status quo, which will certainly lead to a government shutdown if no agreement is reached.

In general, the SQ outcome to a negotiation need not be the least-favored option for all parties, but this would be the case for the 2018–19 U.S. budget negotiations modeled here, where a status quo deadlock is associated with a government shutdown.

To summarize:

• A: Preferred by Democrats over options B and SQ
• B: Preferred by Republicans over options A and SQ
• SQ: Negotiations remain deadlocked and government shuts down

Ideally, a settlement should be both fair and efficient. A fair settlement is one without an a priori bias in reaching it. An efficient settlement is one for which no other settlement would be preferred by both parties. Nash provides a scheme that derives a unique solution, both fair and efficient.

The Nash scheme begins with each party assigning a numerical utility to each of the possible settlement outcomes. An ordered pair of the form (d,r) would then be associated with each outcome, where d and r denote the worth of the outcomes to Democrats and Republicans, respectively. If Democrats favor outcome A with coordinates (d₁, r₁) over outcome B with coordinates (d₂, r₂) and Republicans favor the opposite, it would follow that d₁ > d₂ and r₁ < r₂.

We may also assume that if Democrats are indifferent to payoff (d, r) and a lottery with probability p of payoff (d₁, r₁) and probability 1 – p of payoff (d₂, r₂), then d = pd₁ + (1 – p)d₂. A similar assumption applies to Republicans. A possible agreement or resolution would be one of A, B, SQ, or a random lottery combination of the three.

The utility function used by a party to assign value to outcomes is to reflect the party’s relative preferences for the outcomes. In this sense, the functions used and utilities assigned are not unique and fall into equivalence classes. For A, B, and SQ as above, say Democrats assign utilities 1, 0, –1 respectively, indicating the order of preference A ≻ B ≻ SQ as well as Democrats’ indifference to outcome B and a lottery with equiprobable outcomes A and SQ.

However, assigning 5, 1, –3 to A, B, and SQ, respectively, conveys identical information. In general, two utility functions U₁ and U₂ are considered equivalent by a utility transformation if there constants α > 0 and β such that U₂ = αU₁ + β exist. In this example, multiplying the first set of utilities by 4 (α = 4) and then adding 1 (β = 1) yields the second set.

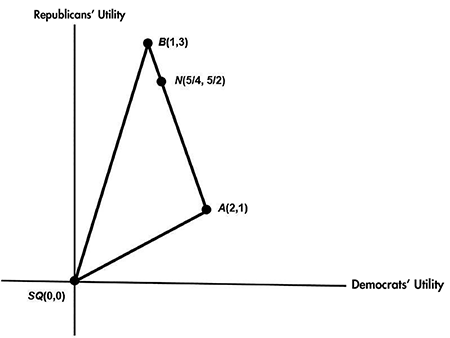
We could assume that 1, 0, –1 are utilities assigned by Democrats to A, B, and SQ, respectively, indicating Democrats’ order of preference A ≻ B ≻ SQ. Say Republicans assign –1, 1, –2, respectively, indicating Republicans’ order of preference B ≻ A ≻ SQ. We can characterize each of the three possible outcomes to the negotiation by the ordered pairs A(1, –1), B(0, 1), and SQ(–1, –2). For convenience, transform all utilities by adding 1 to all Democrats’ utilities and 2 to Republicans’ utilities, translating all utilities so the status quo point SQ is now located at (0, 0), as shown in Figure 1. No information is lost with respect to the parties’ relative preferences.

In addition to the three outcomes A, B, and SQ, additional expected outcomes can be achieved by a random lottery, with probabilities assigned to each actual outcome. For the preceding example, assume we assign to A, B, and SQ the probabilities 1/2, 1/3, and 1/6 respectively. One outcome is then selected by random lottery. The expected outcome (or payoff) to the parties would be E = (1/2)(2, 1) + (1/3)(1, 3) + (1/6)(0, 0) = (4/3, 3/2), a point in the interior of the Figure 1 triangle. This triangle, including its interior is called the payoff polygon. It is defined as the smallest convex set containing the actual outcomes. It represents all outcomes graphically, including expected outcomes associated with random lotteries.

Nash’s Arbitration Solution

Nash believes the fair and efficient agreement (solution, resolution), represented by a point in the payoff polygon, should satisfy these five conditions, or axioms. We call this the Nash point and denote it such as N(d*, r*). From here, we assume the status quo point SQ is (0, 0), since a transformation of the utilities can always achieve this result.

Axiom 1 (rationality): The Nash point N(d*, r*) should be such that d* ≥ 0 and r* ≥ 0. That is, neither party should accept a negotiated settlement less than what they would receive if negotiations were to fail and result in an impasse (SQ).

Axiom 2 (Pareto optimality): There should be no point (d, r) in the payoff polygon where d > d* and r ≥ r* or d ≥ d* and r > r*. This guarantees the efficiency of N.

Axiom 3 (invariance under utility transformations): Consider payoff polygons P and Q related by a utility transformation. The Nash points of each should be related by the same utility transformation.

Axiom 4 (symmetry): If the payoff polygon is symmetric about the line r = d, then N should be on this line. This is a requirement of fairness, eliminating discrimination.

Axiom 5 (independence of irrelevant alternatives): Suppose that N is the Nash point solution for payoff polygon Q. Let P be a payoff polygon that is completely contained in Q which contains both (0, 0) and N. Then N should also be a Nash point solution for P.

Theorem (Nash): One and only one point N(d*, r*) in the payoff polygon satisfies the five axioms. It is given for each of three possible cases:

1. If there are no points in the payoff polygon where d > 0 or r > 0, let N = SQ(0, 0).

2. If d = 0 and r > 0 throughout the payoff polygon let N = (0, r_max).

Similarly, if d > 0 and r = 0 throughout the payoff polygon let N = (d_max, 0).

3. If there are points in the payoff polygon where both d and r are positive, let N be the point where the product dr is maximized.

Proof

The first two cases are self-evident. For Case 3, we note the payoff polygon is closed, bounded, and convex. That means there is a unique point (λ₁, λ₂) in the payoff polygon where dr is maximized. Ultimately, this point would be N(d*, r*), the Nash solution point for Case 3, because it is the only point in the payoff polygon that satisfies all five axioms.

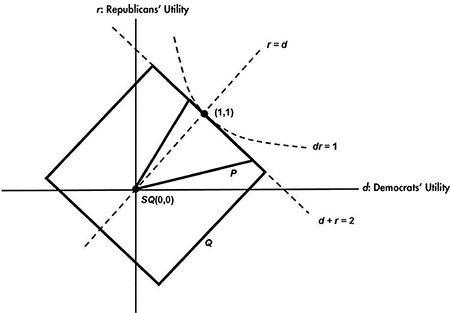
For Case 3, use Axiom 3 to change the utility scales for the parties so (λ₁, λ₂) is transformed to (1, 1). This is done by multiplying d by 1 / λ₁ and r by 1 / λ₂. Let P denote the transformed polygon where dr is now maximized at (1, 1). By Axiom 3 and the product maximizing nature of (1, 1), polygon P lies entirely on or below the upper branch of the hyperbola dr = 1, as shown in Figure 2. The vertex of the hyperbola is (1, 1) and the equation of the tangent line at this point is d + r = 2. Being convex, P must lie on or below this tangent line, for if not, there would be points in P such that dr > 1 · 1 = 1.

Now enclose P in a large square Q with one edge of Q on the tangent line so Q is symmetric about the line r = d. See Figure 2.

According to Axioms 1, 2, and 4, (1, 1) is the only point satisfying the Nash axioms for the large square region Q and must therefore be the unique Nash point solution for Q. Axiom 5 requires that (1, 1) also be the Nash solution point for the embedded payoff polygon P. From Axiom 3 we conclude for the original payoff polygon that N(d*, r*) is the point where dr is maximized. It is the unique, fair, and efficient solution because no other payoff point on or within the original payoff polygon satisfies the five Nash axioms. This completes the proof.

When applied to the example given (Figure 1), it is easily shown that dr is maximized at d* = 5/4, r* = 5/2 yielding the Nash solution point N(5/4, 5/2). This point lays on line segment AB, three-fourths of the way from A to B, as shown in Figure 1. It is achievable by a lottery of outcomes A and B, having probabilities 1/4 and 3/4 respectively, or by tossing a biased coin where the coin’s side associated with A has a probability of 1/4.

Limitations and Other Caveats

A technical objection relates to the seemingly innocuous Axiom 5: Independence of Irrelevant Alternatives (IIR).

While dining at your favorite restaurant, you see the menu offers beef, chicken, or fish as a main course. You decide on beef. When your waiter arrives, you are apologetically told that fish is not available this evening.

Will beef remain your preference? Of course it will! You prefer beef to chicken, with fish being irrelevant.

Admittedly, one might argue that levels of aspiration and other psychological considerations can play a role in determining preferences. Under these circumstances, the addition or deletion of available options may indeed alter relative preferences.

Another theoretical limitation of the process involves that of either party providing false information about their utilities to finesse the outcome in their favor and corrupt the entire process. However, lying can produce an inferior (Pareto) outcome to the lying party, with no guarantee of improving the party’s position. (A full discussion appears in Philip D. Straffin’s Game Theory and Strategy.)

Lastly, a coin toss, lottery, or any form of random outcome generation may not reflect the will of the people when democratic processes are involved, such as U.S. government budget negotiations. Should the flip of a coin do the thinking for a matter of great consequence, such as adoption of the U.S. federal budget? In defense of randomizing, note that the mathematical expectation of the lottery to both parties exceeds that of the status quo. Why not choose by a lottery or coin toss and move on?

Sometimes an arbitrary decision is far better than no decision at all. Analogies can be made to sports, where the toss of a coin or the spin of a tennis racket is used to determine how the game will start. Close calls made by referees are effectively arbitrary due to visual limits. Jump balls in basketball and face-offs in hockey have virtually random outcomes, although some skill by the players is required. In all cases, players and fans understand the decision might go either way, but above all, a decision is required for the game to proceed.

Drawing lots is not new to politics, nor something that only happened in the past. In 2018, a lottery was held to determine the winner of a tied Virginia House of Delegates election. Virginians used a similar lottery to break an election tie in 1971.

Discussion

Can politics be mathematized? It would be naïve to suggest that the simple scheme of Nash resolves all negotiation deadlocks such as the 2018 U.S. government shutdown. Despite the noted objections, the Nash solution is compelling and should be considered. It is efficient and fair, costs almost nothing to implement, and eliminates the concern of a party having to back down on one or more of the issues being negotiated. In addition, there is a surprising additional psychological benefit to using a randomizing device to make decisions.

Faced with a tough decision? Flip a coin to decide. Even before the coin lands, during that brief moment, the coin is spinning in the air, your subconscious will tell you what you really want. When rationality fails, trust your heart.

If Democrats and Republicans were to assign numerical utilities to their preferences and agree to accept an outcome as determined by chance lottery, both parties would achieve a better understanding of the relative importance of their objectives.

In an address to the nation on March 8, 1982, United States President Ronald Reagan urged Congress to “…get off the dime and adopt the deficit-reducing budget.” Once off the dime, Congress might consider tossing it to move things along.

Further Reading

Luce, R.D., and Raiffa, H. 1985. Games and Decisions, New York: Dover Publications, Inc.

Polgreen, P. 1992. Nash’s arbitration scheme applied to a labor dispute. UMAP Journal 13:25–35.

Straffin, P. 1993. Game Theory and Strategy, Washington, DC: Mathematical Association of America.

About the Author

Leonard Wapner has taught mathematics at El Camino College in Torrance, California, since 1973. He received his BA and MAT degrees in mathematics from the University of California, Los Angeles. He is the author of The Pea and the Sun: A Mathematical Paradox and Unexpected Expectations: The Curiosities of a Mathematical Crystal Ball. His writings about mathematics education have appeared in the Mathematics Teacher (National Council of Teachers of Mathematics) and AMATYC Review (American Mathematical Association of Two-Year Colleges).

Back to Top