Mandatory Drug Testing in the Canadian Workplace
A Note on the Recent Supreme Court Decision and Its Effect on the Misclassification Rate of Non-Drug Users
In 2013, the Supreme Court of Canada ruled that firms must have reasonable cause to test employees for alcohol and drug use—even when the workplace is judged to be dangerous. Essentially, management must have good evidence that an employee is a drug or alcohol user before it can subject an employee to a test.
The pros and cons of mandatory drug testing are well known and hence there is no need to consider the full debate here. I want to focus on one important aspect of that debate—the misclassification rate of non-drug users (NDUs). It is well known that drug tests are not perfect. In some cases, drug users (DUs) go undetected, and in others, NDUs can test positive. I’ll argue that, relative to a policy of mandatory testing, a policy of reasonable cause testing lowers the misclassification rate of NDUs substantially.
This work is close in spirit to Charles D. Feinstein’s 1990 article “Deciding Whether to Test Student Athletes for Drug Use.” Feinstein analyzed whether a university ought to adopt a mandatory drug-testing policy for its student athletes. In his work, Feinstein explained how an accurate test employed on a population characterized by low incidence of drug use could lead to NDU misclassification rates that are unacceptably high. Based on his work, the university chose not to introduce mandatory testing.
I will make a variation of his argument here. I contend that the incidence of drug use among those selected for Reasonable Cause Testing would be high—and that this can lower the NDU misclassification rate by an order of magnitude relative to the rate in a Mandatory Testing regime.
The Supreme Court Decision
The Supreme Court decision has its origins with Perley Day, a member of the Communications, Energy and Paperworkers Union of Canada, Local 30, and an employee of Irving Pulp and Paper Limited. In 2006, Irving unilaterally adopted a drug-testing policy in which 10% of employees in “safety sensitive” positions would be tested for drug and alcohol use each year. Day, a teetotaler since 1979, was tested for alcohol, and his breathalyzer test indicated a blood alcohol level of zero. Subsequent to this test, the union filed a grievance on Day’s behalf.
The grievance first went to arbitration. The arbitration board heard the following evidence:
1. Over a period of 15 years, between 1991 and 2006, there were eight documented incidents of alcohol consumption or impairment at the workplace, and none of these resulted in any workplace injury or “near miss.”
2. Between the time the testing policy was introduced and the time the arbitration was heard in December 2008, 22 months later, not a single employee had tested positive.
The board interpreted this evidence as indicative of no problem with substance abuse at the Irving mill. It concluded that the privacy of workers took precedence over any benefit that mandatory testing would have on workplace safety, and therefore allowed the grievance.
Upon judicial review at both the first level (the Court of Queen’s Bench of New Brunswick) and second level (the New Brunswick Court of Appeal), the arbitration board’s decision was rejected. This brought the case to the Supreme Court of Canada. Justice Abella, for the majority, wrote this:
… [A]n employer may only discharge or discipline an employee for “just cause” or “reasonable cause”—a central protection for employees. As a result, rules enacted by the employer as a vehicle for discipline must meet the requirement of reasonable cause…
The Supreme Court concurred with the finding of the arbitration board that there was no evidence of a substance abuse problem at the Irving Mill. Under the principle of reasonableness, the court found in favor of Day and the union. Interestingly, the Canadian Broadcasting Corporation reported in 2013 that Irving management felt there was a problem. Clearly, the interpretation of data is in the eye of the beholder.
Accuracy of Drug Testing
When testing for illicit drugs, there is typically a two-stage procedure. First, there is a screen, and if a subject tests positive, a more accurate test is used to confirm or challenge the first test. The most prevalent screen is an immunoassay (a test measuring the presence of a specific substance) applied to a sample of the subject’s urine. If the person has ingested an illegal drug for which the immunoassay is designed, and the drug has not yet cleared the person’s system, the immunoassay will detect a metabolite (a byproduct of the drug) in the urine and conclude a positive result.
If the screen is positive, most drug-testing procedures require that the confirmation be done with gas chromatography/mass spectrometry (GC-MS). This is a very accurate test, but it’s expensive.
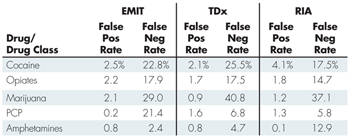
For “A Comparison of Urinalysis Technologies for Drug Testing in Criminal Justice,” published in 1991, Christy Visher studied the chemical accuracy of three immunoassays: Enzyme Multiplied Immunoassay (EMIT), Fluorescence Polarization Immunoassay (TDx), and Radioimmunoassay (RIA). For each, GC-MS was used to confirm the results. The results are shown in Table 1. Note that the false positive rates are low and generally much lower than the false negatives.
To be sure, there is no drug-testing procedure that is foolproof. Regardless of how accurate the chemistry is, there is still the possibility of human error in the administration of the test.
The Feinstein Argument
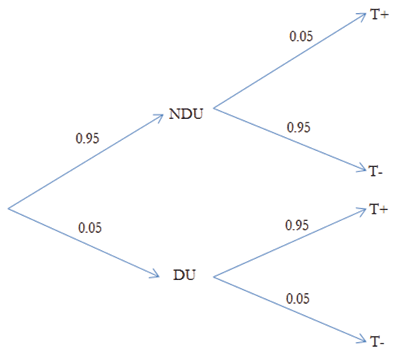
To make his point about NDU misclassification rates in mandatory testing programs, Feinstein assumed a particular incidence of drug use within the population being tested and then a symmetric false positive and false negative rate. Here is one of his examples: Suppose that 5% of a population is made up of DUs, the false positive rate is 5%, and the false negative rate is 5%. Using Bayes Rule, he calculated the probability a subject is a NDU given a positive test. The probability tree for this calculation is shown in Figure 1.
By Bayes Rule, we have that
That is, the proportion of NDUs among those who test positive is 50%. This is indeed a surprising result and suggests that a relatively accurate test might not be that good if the incidence of drug use in the population is low.
Before proceeding, I want to make a couple of qualifying remarks. First, I did not model a screen/confirmation test explicitly. I am assuming that the tree takes into account the possibility that a screen/confirmation was done and also that it takes into account any dependence between these two tests. Second, the specific numbers I used are Feinstein’s and are not crucial to the point I am going to make.
One way to understand the Feinstein result is to assume that 10,000 subjects are tested and then look at the relative proportions of NDUs and DUs who test positive. These numbers are shown in Figure 2. Note that there are a total of 475 + 475 = 950 positive tests; of these, half are NDUs.
Now to my point. If an organization employs reasonable cause testing, management would ask for a drug-test only if it had good evidence that an employee was a DU. This evidence could be based on reports by co-workers; uncharacteristic behavior; circumstantial evidence like drug paraphernalia discovered in a company locker; an interview of the employee; etc. Once a supervisor is in possession of such evidence, we assume organizational protocol will be followed before the employee is confronted. For instance, in the Canadian Forces, if a commander receives evidence of a soldier’s drug use, he is obligated to speak with lawyers in the Judge Advocate General’s Office to determine whether he has sufficient cause to require a drug test. A priori, we would not expect the manager to have a bias against an employee, and hence he or she would act only in the face of good, solid evidence.
This simple observation changes the calculation considerably. We no longer have a general population. Rather, we have one where, if management is doing its job properly, there should be a high incidence of drug use among those sent for testing. To put some numbers to it, suppose the incidence of drug use under a reasonable cause testing regime is 95%. Then recalculating the misclassification rate, we have the following:
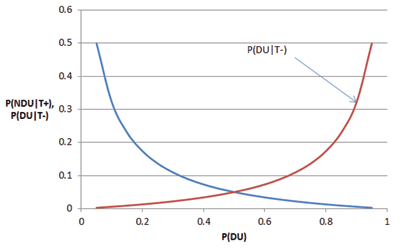
or 3 in 1,000. This is substantially lower than the 50/50 result with mandatory testing. In Figure 3, I’ve included a plot of how P (N DU |T +) changes for various proportions of DUs in the population being sampled. Note that as this proportion increases, P (N DU |T +) falls precipitously.
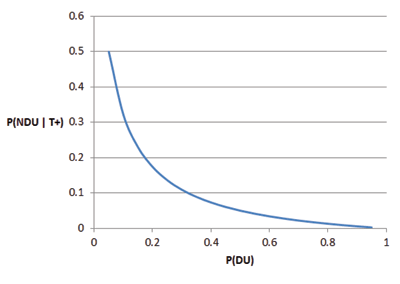
Figure 3. P (DN U |T +) versus P (DU). This graph shows the probability an NDU tests for various incidences of drug use in the population sampled.
I’ve done a considerable sensitivity analysis on this result for reasonable incidences of demand and drug testing accuracies—including the case where the false positive and false negative rates are different. In all cases, the chance of misclassifying an NDU with mandatory testing is a couple of orders of magnitude larger than it is with reasonable cause testing.
Detecting Drug Users
While the main point of this paper involves the effect of a testing regime on the chances of convicting an innocent man, there is another side of the coin. Any consideration of drug testing policy ought to consider the other misclassification error, P (DU |T −), the proportion of DUs who escape detection as a result of the inaccuracy of the test.
Assuming the testing accuracies defined above, this proportion gets higher as P (DU) gets higher. A plot of P (DU |T −) versus P (DU) is shown in Figure 4. Note that it is increasing in P (DU) and symmetric with P (N DU |T +) about P (DU) = 0.5. Consequently, with reasonable cause testing, while the P (N DU |T +) is lowered, it is also true that P (DU |T −) increases.
Unfortunately, this is a rather narrow analysis of the chances that DUs are misclassified. There is also the chance that with reasonable cause testing, DUs are not tested at all. A proper comparison of the two regimes would require a more detailed model—one that considered, at minimum, the probability that a DU can mask his or her drug use over an extended period, and whether this drug use resulted in a significant incident that the DU had successfully masked. But this is a problem for another paper with a more detailed model.
Conclusion
I considered the recent Supreme Court decision regarding the introduction of mandatory drug testing in the workplace. The court has taken the position that employers must demonstrate reasonable cause before an employee can be tested for drugs. I’ve argued here that the court’s decision has the unintended salutary effect that the misclassification rate for non-drug users is lowered substantially. While this result has no bearing on the logic of the court’s decision, it’s an important consideration in an organization’s design of its drug-testing policy.
Further Reading
CBC News. 2013. Workplace random alcohol tests rejected by top court.
Feinstein, C. D. 1990. Deciding whether to test student athletes for drug use. Interfaces 20(3):80-87.
Supreme Court of Canada. 2013. Reasons for judgment: Communications, Energy and Paperworkers Union of Canada, Local 30 (Appellant) and Irving Pulp & Paper, Limited (Respondent).
Visher, C. 1991. A comparison of urinalysis technologies for drug testing in criminal justice. National Institute of Justice Research in Action, Washington DC: Department of Justice.
About the Author
W. J. Hurley is a professor in the department of mathematics and computer science at the Royal Military College of Canada. His research interests are in decision analysis, game theory, and the design of MAC protocols in wireless networks.


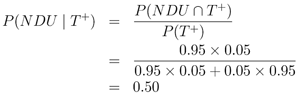

Dear Dr. Hurley,
Have you considered how retesting might impact misclassifications? I know most of the Bayes predictions require independence between tests and that usually is hard to establish without a gold standard, but I have been using G theory to look at dependence, and found that it provides a solution and better outcomes.
Clare
Clarence D. Kreiter, PhD
Professor
Department of Family Medicine
OCRME
University of Iowa
Iowa City, IA 52242
http://www.medicine.uiowa.edu/dept_primary_apr.aspx?appointment=Family%20Medicine&id=kreiterc